排序算法之归并排序
前言
归并排序是先进排序的其中之一,本篇文章是我在学习过程中,对于归并排序的理解,以及归并排序的模板。
归并排序概述
归并排序主要思想是基于分治法的思想,大致流程为:
-
将一个数组分为两个尽量等长的数组,然后去排序这两个数组
-
这很明显也是一个递归调用,我们在递归的时候,直到剩下一个元素暂停
-
然后再将排序好的数组依次合并即可
归并排序图文讲解
我们给了一个长度为8的数组

将该数组拆分
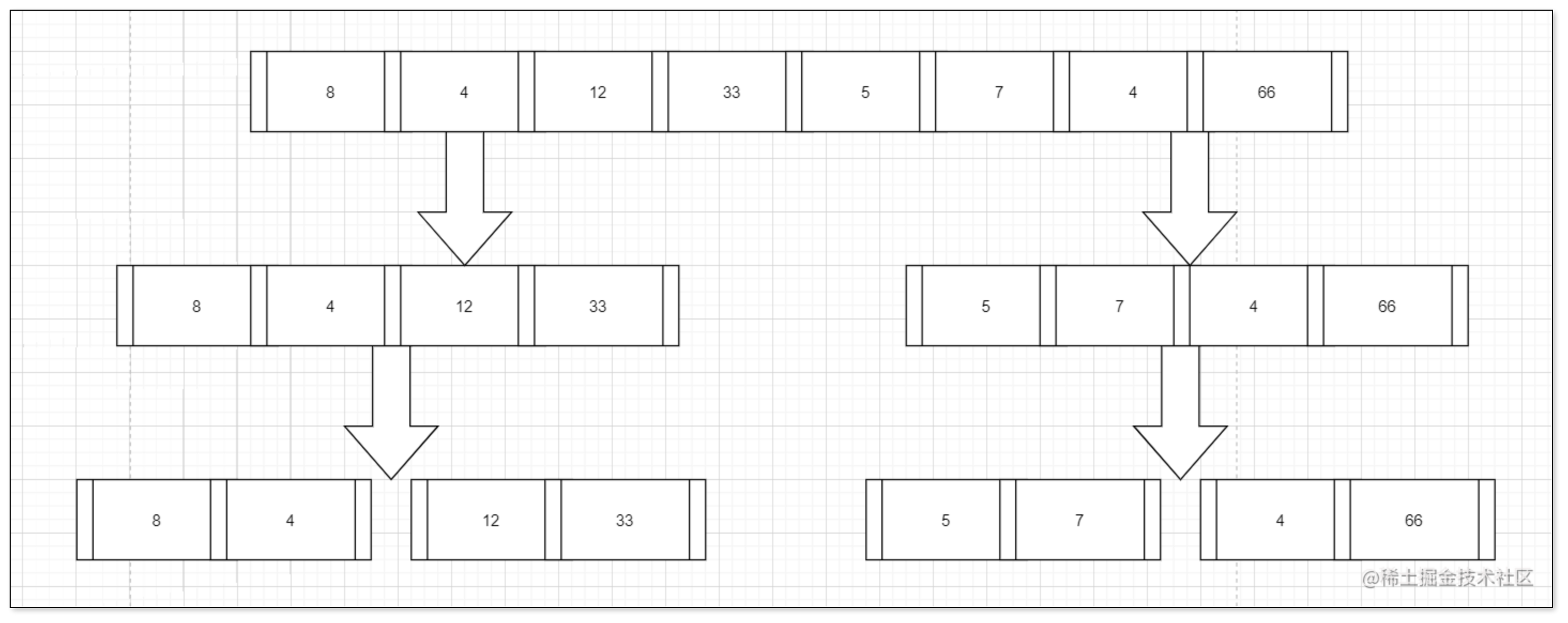
拆分之后我们进行排序
我们按照这个思想继续
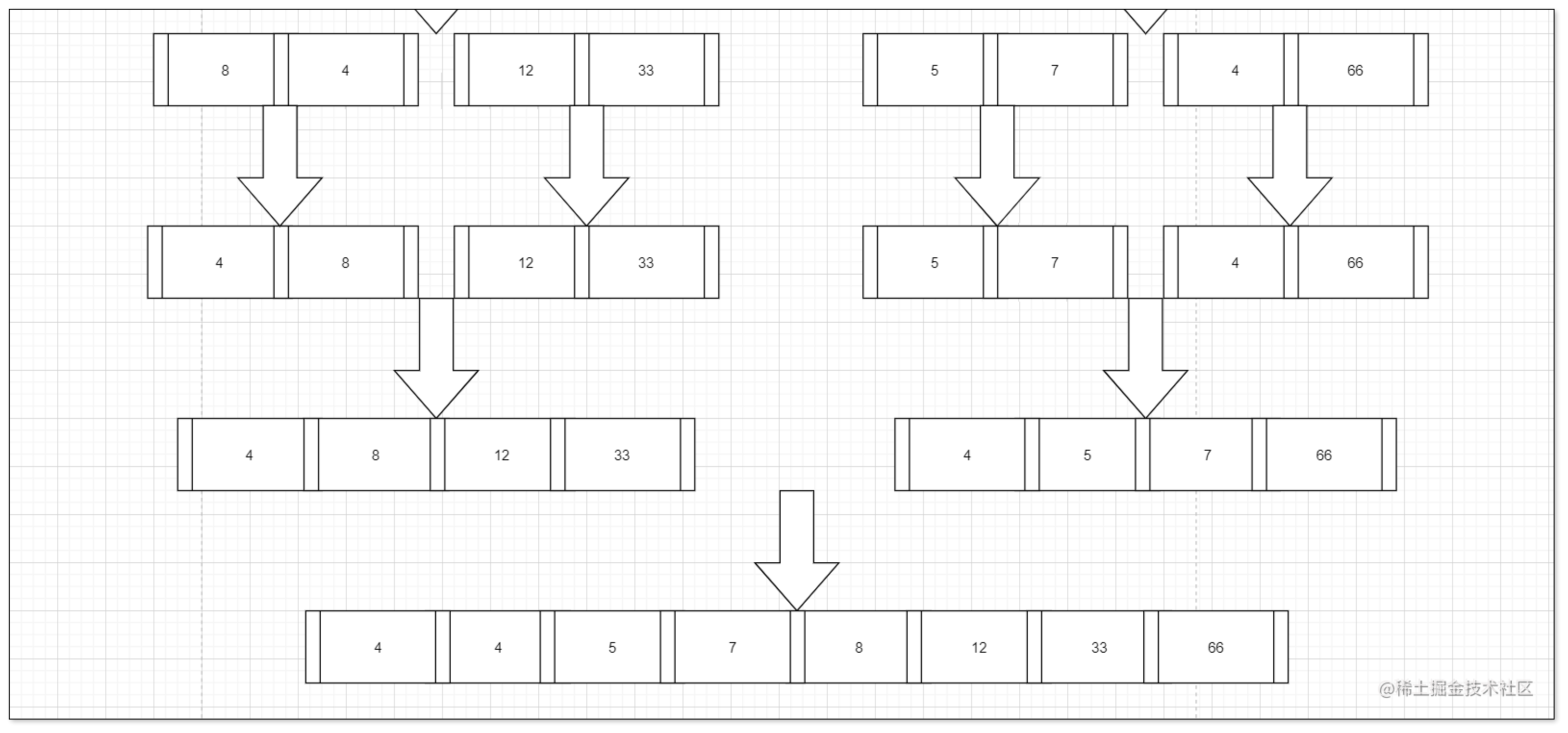
归并排序代码实现
public static void sort(int[] nums,int left,int right){
if(left >= right)return;
int middle = (left + right) / 2;
sort(nums, left, middle);
sort(nums, middle + 1, right);
//合并数组???
int[] temp = new int[right - left + 1];//暂存需要合并的区间
for (int k = left; k <= right; k++) {
temp[k - left] = nums[k];
}
int i = 0;//定义两个指针分别指向左右子数组的首个元素
int j = middle - left + 1;
for (int k = left; k <= right; k++) {
if(i == middle - left + 1){
nums[k] = temp[j++];
}else if(j == right - left + 1 || temp[i] <= temp[j]){
nums[k] = temp[i++];
}else{
nums[k] = temp[j++];
}
}
}
static void mergeSort(int[] nums, int l, int r) {
// 终止条件
if (l >= r) return;
// 递归划分
int m = (l + r) / 2;
mergeSort(nums, l, m);
mergeSort(nums, m + 1, r);
// 合并子数组
int[] tmp = new int[r - l + 1]; // 暂存需合并区间元素
for (int k = l; k <= r; k++)
tmp[k - l] = nums[k];
int i = 0, j = m - l + 1; // 两指针分别指向左/右子数组的首个元素
for (int k = l; k <= r; k++) { // 遍历合并左/右子数组
if (i == m - l + 1)
nums[k] = tmp[j++];
else if (j == r - l + 1 || tmp[i] <= tmp[j])
nums[k] = tmp[i++];
else {
nums[k] = tmp[j++];
}
💬 评论区